|
|
|
|
|
|
|
|
|
|
|
|
Noah A Rosenberg
+1 650 721 2599 (office phone)
+1 650 724 5122 (lab phone)
+1 650 724 5114 (fax)

Mailing address
Department of Biology
Stanford University
371 Jane Stanford Way
Stanford, CA 94305-5020 USA
Last modified 7-18-2024 |
|
We are a mathematical, theoretical, and computational lab in genetics
and evolution. Research in the lab addresses problems in evolutionary
biology and human genetics through a combination of mathematical
modeling, computer simulations, development of statistical methods, and
inference from population-genetic data.
Read more...
RECENT NEWS
7-18-2024 — Two papers appear in the proceedings of the
Analysis of Algorithms conference (AofA 2024).
Michael Doboli evaluates
the large-n behavior of the minimal Colin-Plazzotta rank of an
rooted unlabeled binary tree with an increasing number of
leaves n, finding that it has a periodic pattern characteristic
of "divide-and-conquer" recurrences. The paper solves a problem posed by
[189]. Lily Agranat-Tamir
studies the number of
rooted binary unlabeled galled trees with a fixed number of galls, finding
an equivalence of the exponential order with that of the number of rooted
binary unlabeled trees with no galls. The paper builds on [229].
4-28-2024 — Lily
Agranat-Tamir extends
a model of genealogical ancestry in an admixed population, in order to
understand how many genetic ancestors an admixed individual
possesses in each of the source populations at a given moment back in
time. In an application to African Americans, the study estimates that
the mean number of African genetic ancestors is 162 and the mean
number of European genetic ancestors is 32, where an African or
European genealogical ancestor is tabulated as such if the person is
the most recent African or European along a genealogical line to the
descendant. Jazlyn Mooney has also contributed to the study,
which builds on her recent work
[215].
3-27-2024 — A
study led by Lily
Agranat-Tamir enumerates the rooted binary unlabeled galled trees
with n leaves and the rooted binary unlabeled galled trees
with n leaves and g galls. The approach focuses on
"normal" galled trees, the same class of phylogenetic networks studied in
a recent enumeration of labeled histories for galled trees
[212].
3-4-2024 — The Hill numbers are a family of biodiversity
measures describing the diversity of ecological communities. A
new study examines
the dependence of the Hill numbers on the most abundant species in a
community. The results show that taking into account this abundance
can change one's perspective about which of a set of communities has
the greatest biodiversity.
2-8-2024 — A
new study examines
coalescence times, runs of homozygosity, and identity by descent on
the X chromosome, predicting the relationship between ROH on the X
chromosome and ROH on the autosomes. The study finds that in accord
with its mathematical predictions, ROH occupy more of the X chromosome
than the autosomes, and the X-chromosomal excess is close to the
excess that is predicted.
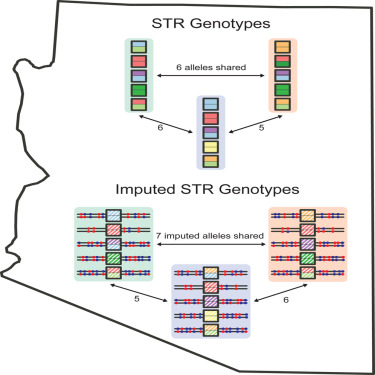
2-3-2024 — What is the probability distribution of the
number of matching alleles between pairs of profiles in a forensic
database? This search for matching profiles in an existing database is
known as an "Arizona search," after an incident in which such a search
was performed in Arizona's database. How does one compute the
distribution of the number of matching alleles when actual forensic
profiles are unavailable? Egor
Lappo introduces
a method for evaluating this probability distribution from imputations
performed on the basis of neighboring loci in samples typed
genome-wide.
 1-7-2024 — Xiran Liu
reports Clumppling, a
new program for aligning replicate solutions in mixed-membership
unsupervised clustering. The approach extends
beyond Clumpp
and Clumpak,
improving computation time and addressing additional scenarios, all
while addressing a computational biology problem with ideas from
combinatorial optimization and network theory. The method builds on
Xiran's earlier mathematical models of the cluster alignment problem
[216].
12-15-2023 — If all the games in a
single-elimination sports tournament are played sequentially in
the same arena, in how many possible sequences can the games be
played? Evolutionary biology has the answer. A
new study with
undergraduate Matt King explores the connections between
game sequences in sports tournaments and labeled histories in
mathematical phylogenetics, solving new problems that permit
simultaneous games across multiple arenas — or simultaneous
bifurcations in evolutionary trees.
[Stanford
Report]
12-10-2023 — The mean allele-sharing dissimilarity between
members of a population sometimes exceeds the mean allele-sharing
dissimilarity between members of that population and members of a
second population. A study led by PhD student Xiran Liu, with
help from undergraduates Zarif Ahsan and Tarun
Martheswaran, solves for the allele-frequency conditions that
generate this counterintuitive phenomenon.
11-16-2023 — How do chess players choose their
strategies? Egor Lappo analyzes millions of master-level games
from 1971-2019 in the framework of cultural evolution. Modeling the
transmission of chess openings from one year's games to the next, he
uncovers evidence of
that the mechanisms of cultural evolution affect cultural transmission
of move choice in chess — mechanisms including success
bias, anti-conformity bias, and prestige bias.
[Stanford Report]
11-2-2023 — Jaehee Kim extends the technique of
genetic record matching, showing in a
new paper that the
method can achieve much higher levels of accuracy than in previous
analyses [148]
[159]. The study considers the
case in which links are sought between SNP profiles from low-quality
DNA and STR profiles in forensic STR databases, as might occur in
certain forensic settings involving trace DNA samples, degraded
remains, or ancient DNA.
10-26-2023 — In a new investigation linking mathematical
results on population-genetic statistics to diversity statistics in
ecology, Maike Morrison
investigates how
the Shannon entropy statistic for measuring the diversity of
ecological communities depends on the abundance of the ith
most abundant taxon. The analysis, which considers data from corals
and sponge microbiomes, relies on majorization-based inequalities from
previous work in the lab [158].
10-24-2023 — Egor
Lappo introduces
a new conception of the ancestral configurations that describe the
relationship between gene trees and species trees, viewing them
through the lattice structure of a partial order. The lattice
sturcture can be mined for many results on ancestral configurations,
connecting to previous work of Filippo Disanto
[152] as well as to
work from the lab on labeled histories
[212].
9-22-2023 — The unlabeled binary rooted trees can be
bijectively associated with the positive integers by a mapping that
proceeds recursively from the tree root. Alessandra Maranca
shows in a
new paper that
unlabeled multifurcating rooted trees can also be bijectively
associated with the positive integers. The paper provides the
bijective construction for two types of multifurcating rooted trees:
strictly k-furcating, and at-most-k-furcating.
9-17-2023 — Mixed-membership unsupervised clustering is
a central part of population-genetic data analysis. A
new paper led by Xiran
Liu studies misalignment cost for replicate clustering analyses
under a Dirichlet model of cluster membership vectors. The paper
describes as a function of model parameters the cost for misaligned
permutations compared to an optimal permutation. The work assists in
understanding properties of the permutations identified by methods
like CLUMPP and Clumpak
[43]
[130].
8-18-2023 — In a
new study, Filippo Disanto et
al. obtained asymptotic distributions for the total number of
ancestral configurations for matching gene trees and species trees,
under the Yule and uniform models describing the labeled tree
topology. The results extend Filippo's earlier work on ancestral
configurations
[152]
[161], particularly
computations focused on asymptotic distributions of root ancestral
configurations [211].
7-10-2023 — Jazlyn Mooney describes
a model that
examines genealogical lines in an African-American genealogy traced from
1960-1965 back until founding source populations are reached on each
branch of the family tree. The model estimates that the mean number of
African genealogical lines in a typical genealogy is 314 and the mean
number of European genealogical lines is 51. Lily Agranat-Tamir
also contributed to the study, which builds on an earlier admixture model
papers from the lab [82].
[Genes to Genomes]
[Stanford Report]
1-7-2024 — Xiran Liu
reports Clumppling, a
new program for aligning replicate solutions in mixed-membership
unsupervised clustering. The approach extends
beyond Clumpp
and Clumpak,
improving computation time and addressing additional scenarios, all
while addressing a computational biology problem with ideas from
combinatorial optimization and network theory. The method builds on
Xiran's earlier mathematical models of the cluster alignment problem
[216].
12-15-2023 — If all the games in a
single-elimination sports tournament are played sequentially in
the same arena, in how many possible sequences can the games be
played? Evolutionary biology has the answer. A
new study with
undergraduate Matt King explores the connections between
game sequences in sports tournaments and labeled histories in
mathematical phylogenetics, solving new problems that permit
simultaneous games across multiple arenas — or simultaneous
bifurcations in evolutionary trees.
[Stanford
Report]
12-10-2023 — The mean allele-sharing dissimilarity between
members of a population sometimes exceeds the mean allele-sharing
dissimilarity between members of that population and members of a
second population. A study led by PhD student Xiran Liu, with
help from undergraduates Zarif Ahsan and Tarun
Martheswaran, solves for the allele-frequency conditions that
generate this counterintuitive phenomenon.
11-16-2023 — How do chess players choose their
strategies? Egor Lappo analyzes millions of master-level games
from 1971-2019 in the framework of cultural evolution. Modeling the
transmission of chess openings from one year's games to the next, he
uncovers evidence of
that the mechanisms of cultural evolution affect cultural transmission
of move choice in chess — mechanisms including success
bias, anti-conformity bias, and prestige bias.
[Stanford Report]
11-2-2023 — Jaehee Kim extends the technique of
genetic record matching, showing in a
new paper that the
method can achieve much higher levels of accuracy than in previous
analyses [148]
[159]. The study considers the
case in which links are sought between SNP profiles from low-quality
DNA and STR profiles in forensic STR databases, as might occur in
certain forensic settings involving trace DNA samples, degraded
remains, or ancient DNA.
10-26-2023 — In a new investigation linking mathematical
results on population-genetic statistics to diversity statistics in
ecology, Maike Morrison
investigates how
the Shannon entropy statistic for measuring the diversity of
ecological communities depends on the abundance of the ith
most abundant taxon. The analysis, which considers data from corals
and sponge microbiomes, relies on majorization-based inequalities from
previous work in the lab [158].
10-24-2023 — Egor
Lappo introduces
a new conception of the ancestral configurations that describe the
relationship between gene trees and species trees, viewing them
through the lattice structure of a partial order. The lattice
sturcture can be mined for many results on ancestral configurations,
connecting to previous work of Filippo Disanto
[152] as well as to
work from the lab on labeled histories
[212].
9-22-2023 — The unlabeled binary rooted trees can be
bijectively associated with the positive integers by a mapping that
proceeds recursively from the tree root. Alessandra Maranca
shows in a
new paper that
unlabeled multifurcating rooted trees can also be bijectively
associated with the positive integers. The paper provides the
bijective construction for two types of multifurcating rooted trees:
strictly k-furcating, and at-most-k-furcating.
9-17-2023 — Mixed-membership unsupervised clustering is
a central part of population-genetic data analysis. A
new paper led by Xiran
Liu studies misalignment cost for replicate clustering analyses
under a Dirichlet model of cluster membership vectors. The paper
describes as a function of model parameters the cost for misaligned
permutations compared to an optimal permutation. The work assists in
understanding properties of the permutations identified by methods
like CLUMPP and Clumpak
[43]
[130].
8-18-2023 — In a
new study, Filippo Disanto et
al. obtained asymptotic distributions for the total number of
ancestral configurations for matching gene trees and species trees,
under the Yule and uniform models describing the labeled tree
topology. The results extend Filippo's earlier work on ancestral
configurations
[152]
[161], particularly
computations focused on asymptotic distributions of root ancestral
configurations [211].
7-10-2023 — Jazlyn Mooney describes
a model that
examines genealogical lines in an African-American genealogy traced from
1960-1965 back until founding source populations are reached on each
branch of the family tree. The model estimates that the mean number of
African genealogical lines in a typical genealogy is 314 and the mean
number of European genealogical lines is 51. Lily Agranat-Tamir
also contributed to the study, which builds on an earlier admixture model
papers from the lab [82].
[Genes to Genomes]
[Stanford Report]
 7-7-2023 — A
new study led by postdoc
alum Paul Verdu deepens the understanding of the admixture
processes taking place on the various islands of Cabo Verde. The study,
like an earlier paper combines
genetic analysis with linguistic analysis of idiolectal variation in the
Kriolu-speaking population. PhD graduate Zach Szpiech contributed
to the project.
6-5-2023 — Danny Cotter reports a
study with an updated method for
measuring the amount of rare and common variation that is shared across
populations. In human data, it provides new calculations and
visualizations for the fundamental result that nearly all human genetic variants are
either common and widely shared or localized and rare, not common in one place
and rare or absent elsewhere.
5-12-2023 — Congratulations to PhD students who have
successfully defended their theses!
7-7-2023 — A
new study led by postdoc
alum Paul Verdu deepens the understanding of the admixture
processes taking place on the various islands of Cabo Verde. The study,
like an earlier paper combines
genetic analysis with linguistic analysis of idiolectal variation in the
Kriolu-speaking population. PhD graduate Zach Szpiech contributed
to the project.
6-5-2023 — Danny Cotter reports a
study with an updated method for
measuring the amount of rare and common variation that is shared across
populations. In human data, it provides new calculations and
visualizations for the fundamental result that nearly all human genetic variants are
either common and widely shared or localized and rare, not common in one place
and rare or absent elsewhere.
5-12-2023 — Congratulations to PhD students who have
successfully defended their theses!
- Danny Cotter, "The effects of relatedness and
sex-biased demographic processes on human genetic variation"
- Xiran Liu, "Computational methods and mathematical measures
for population relationships"
2-14-2023 — "All galls are divided into three or more
parts" — so reports
a study from
Shaili Mathur, describing a recursive decomposition used to
enumerate labeled histories for galled trees. The study is the
first to enumerate labeled histories for a class of phylogenetic
network.
12-13-2022 — A new study by Filippo Disanto
et al. obtains asymptotic
distributions for the number of root ancestral configurations of
matching gene trees and species trees, under the Yule and uniform
models describing the labeled tree topology. The results build on
Filippo's earlier work on ancestral configurations
[152]
[161].
11-15-2022 — Egor Lappo has
been recognized with
honorable mention for the 2023 AMS-MAA-SIAM Frank and Brennie Morgan
Prize for Outstanding Research in Mathematics by an Undergraduate
Student! Congrats to Egor.
11-15-2022 — Egor Lappo extends his analysis of
coalescent trees by producing new
approximate results
for expectations and variances of ratios of tree properties under the
coalescent model. The results extend Egor's earlier analysis of
covariances and correlations of tree
properties [198].
9-12-2022 — In the 200th year since Gregor Mendel's
birth, a historical
commentary discusses Mendel as an icon not only of
genetics, but also of the intersection of mathematics and biology.
9-6-2022 — PhD student Maike Morrison, working
with former postdoc Nicolas Alcala, introduces a
new method for measuring
the variability in membership assignments observed in genetic cluster
analysis. The method relies on a new and surprising use of the
population-genetic statistic FST.
 8-29-2022 — PhD student Danny
Cotter advances the study of
X-chromosomal and autosomal coalescence times in consanguineous
populations. Danny shows that coalescence in X-chromosomal first-cousin
mating models behaves like the standard coalescent, except with a
reduction in coalescence time that depends on the features of
consanguinity. The study builds on three recent studies from the lab on
coalescence in consanguineous populations
[166]
[194]
[195].
7-11-2022
— Rohan Mehta
and collaborator Mike Steel introduce a
general algorithm for
computing the probability of reciprocal monophyly of arbitrarily many
groups in an arbitrary species tree. The study generalizes earlier
computations involving species trees with three and four monophyletic
groups [172], and
with two monophyletic groups in arbitrary species trees
[141].
5-26-2022 — Xiran Liu
and Gili
Greenbaum apply
the Netstruct hierarchical
clustering program to study cultural variation. The analysis, which
adapts a method from population genetics for cultural data, reveals new
features of variation in regional pronunciation in the eastern United
States, folklore motifs and phonemic content of languages worldwide, and
US first names.
5-18-2022 — A team including Julia Palacios, Anand
Bhaskar, and Filippo
Disanto describes
an enumeration of binary trees in each of several categories (ranked
labeled, ranked unlabeled, unranked labeled, unranked unlabeled) that
are compatible with a perfect phylogeny. The enumeration is a
contribution to the study of the
combinatorics
of evolutionary trees.
5-5-2022 — A special issue of Philosophical
Transactions of the Royal Society B Biological
Sciences
with editors Doc Edge, Sohini Ramachandran, and Noah Rosenberg
celebrates
50 years since Lewontin's apportionment of human diversity." The special
issue covers the background and legacy of this important milestone in the
understanding of human genetic variation as well as recent technical
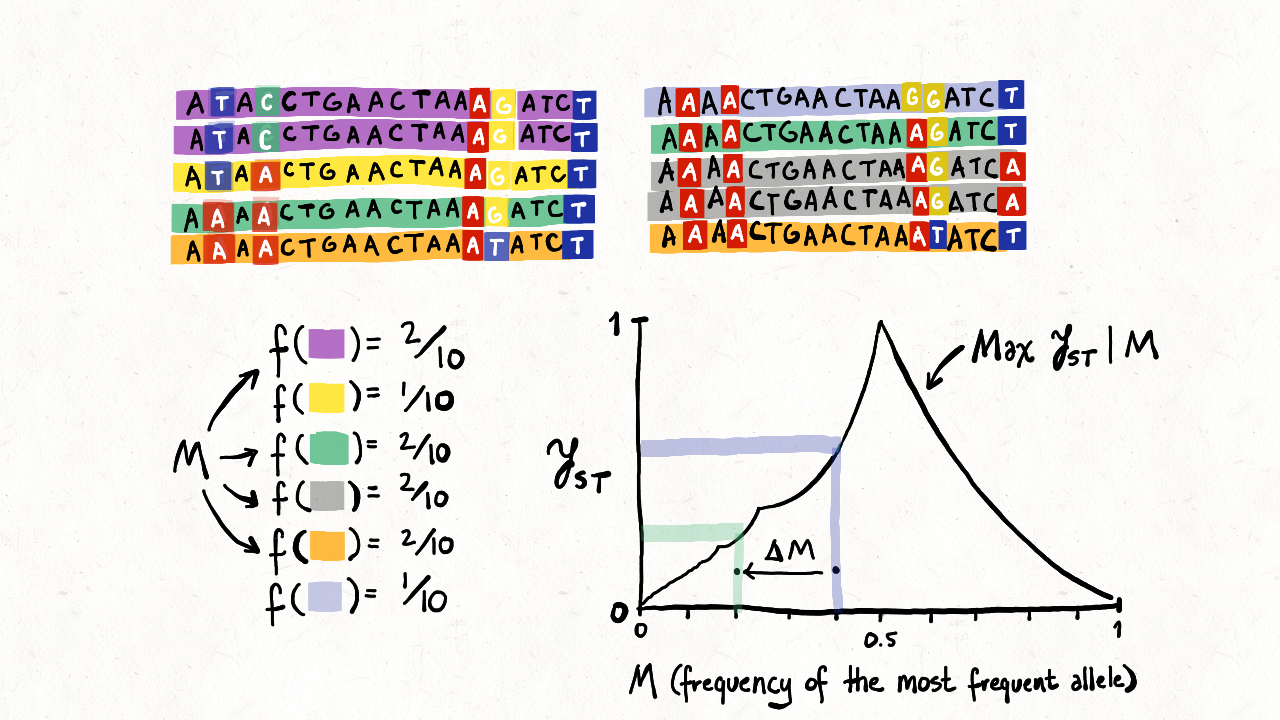
advances that connect to it. In the special issue, Nicolas Alcala
contributes a study
of FST in relation to the frequency of the most
frequent allele for multiallelic loci in multiple populations,
generalizing earlier results for multiallelic loci in two populations
[102] and biallelic loci in
multiple populations
[149].
8-29-2022 — PhD student Danny
Cotter advances the study of
X-chromosomal and autosomal coalescence times in consanguineous
populations. Danny shows that coalescence in X-chromosomal first-cousin
mating models behaves like the standard coalescent, except with a
reduction in coalescence time that depends on the features of
consanguinity. The study builds on three recent studies from the lab on
coalescence in consanguineous populations
[166]
[194]
[195].
7-11-2022
— Rohan Mehta
and collaborator Mike Steel introduce a
general algorithm for
computing the probability of reciprocal monophyly of arbitrarily many
groups in an arbitrary species tree. The study generalizes earlier
computations involving species trees with three and four monophyletic
groups [172], and
with two monophyletic groups in arbitrary species trees
[141].
5-26-2022 — Xiran Liu
and Gili
Greenbaum apply
the Netstruct hierarchical
clustering program to study cultural variation. The analysis, which
adapts a method from population genetics for cultural data, reveals new
features of variation in regional pronunciation in the eastern United
States, folklore motifs and phonemic content of languages worldwide, and
US first names.
5-18-2022 — A team including Julia Palacios, Anand
Bhaskar, and Filippo
Disanto describes
an enumeration of binary trees in each of several categories (ranked
labeled, ranked unlabeled, unranked labeled, unranked unlabeled) that
are compatible with a perfect phylogeny. The enumeration is a
contribution to the study of the
combinatorics
of evolutionary trees.
5-5-2022 — A special issue of Philosophical
Transactions of the Royal Society B Biological
Sciences
with editors Doc Edge, Sohini Ramachandran, and Noah Rosenberg
celebrates
50 years since Lewontin's apportionment of human diversity." The special
issue covers the background and legacy of this important milestone in the
understanding of human genetic variation as well as recent technical
advances that connect to it. In the special issue, Nicolas Alcala
contributes a study
of FST in relation to the frequency of the most
frequent allele for multiallelic loci in multiple populations,
generalizing earlier results for multiallelic loci in two populations
[102] and biallelic loci in
multiple populations
[149].
 3-21-2022 — Alissa Severson and a collaborative
team report a
genetic study of ancient
burial sites and their continuity with modern members of the Muwekma
Ohlone Tribe. The project, a collaboration with the tribal leadership,
finds a component of genetic ancestry that connects two burial sites
separated by hundreds of years with each other and with the modern
tribal members.
[Illinois
News Bureau]
[Stanford
Report]
11-30-2021 — Under the coalescent model, a genealogical tree
possess a series of features: its height, length, sum of external
branches, sum of internal branches, and mean basal branch
length. Egor Alimpiev
has calculated the
covariance and correlation coefficients of all these pairs of random
variables, providing a compendium of existing and new fundamental results for the
coalescent model. The calculation builds on a previous calculation for one of
the pairs considered [154].
11-11-2021 — The Sackin index is one of the most
commonly used measures of tree balance. Undergraduate Matt King
reports a simple new proof
of a result that finds the mean value of the Sackin index across all
labeled topologies on n leaves. The proof makes use of an
identity that has been called by Graham, Knuth & Patashnik a
"remarkable property of the 'middle' elements of Pascal's triangle."
8-24-2021 — For a caterpillar species tree,
undergraduate Egor
Alimpiev studies
coalescent histories in a family of gene trees,
the p-pseudocaterpillar gene trees. For this family, his study
investigates a claim that the number of coalescent histories is affected
by a tradeoff between the number of possible sequences of coalescences
and the number of species tree branches on which those sequences can
take place. He finds a very nice symmetry. The work extends a study by a previous undergraduate in the
lab, Zoe Himwich
[176]
8-24-2021 — PhD student Danny
Cotter continues the
investigation of coalescence times in consanguineous populations,
considering the mean time to coalescence for a pair of lineages on the X
chromosome in each of four first-cousin mating models. He finds that
matrilateral first-cousin mating reduces X-chromosomal coalescence times
to a greater extent than patrilateral first-cousin mating. The work
builds on two studies led by co-author Alissa Severson
[166]
[194].
5-28-2021 —
In a new article led by PhD student
Alissa Severson, the distribution of coalescence times is computed
in a diploid model of a consanguineous population. Using a
separation-of-time-scales approach, the study shows that the time to the
most recent common ancestor for pairs of lineages in separate mating pairs
follows a coalescent model with a reduced effective popualtion size. The
study builds on a previous theoretical study that examined the mean
pairwise coalescence time
[166].
5-25-2021 — Congratulations! Alissa Severson has
successfully defended her PhD, "The effect of relatedness and population
structure on patterns of genomic sharing."
5-21-2021 — Jaehee
Kim, Doc Edge,
and Amy Goldberg report
a study of the decoupling of a
phenotype from admixture levels in an admixed population whose source
populations differed in phenotype. As time proceeds, the phenotype of
an individual comes to reveal less and less information about the individual's
admixture level, particularly if mating occurs randomly in the admixed population. [Stanford
Report]
3-11-2021
— Gili
Greenbaum and Jaehee Kim report a
population-genetic model
of gene drives and their potential to "spill over" from one population to
another. In the model, an engineered gene drive is introduced into a
target population with the goal of overtaking the extant population. Under
what circumstances can the introduced gene drive be prevented from
overtaking genotypes in non-target populations? The study finds a narrow
set of circumstances.
2-8-2021 — Last year
we celebrated
the 50th anniversary of the journal Theoretical Population
Biology. The anniversary came just as the role for mathematical
epidemiology models of COVID-19 began receiving intense attention. A
recent editorial discusses the
connections between decades of population biology modeling and the
COVID-19 pandemic.
2-2-2021 — In
a genome scan of rats in
New York City, former rotation student Arbel Harpak identifies
genes associated with metabolism, diet, the nervous system, and
locomotion as possible targets of natural selection. The results add
to a growing understanding of adaptation in human-commensal species.
12-18-2020 — Colijn & Plazzotta (2018) introduced a
clever new way to associate the unlabeled binary rooted trees with the
positive integers. A
new paper explores the
mathematical properties of the Colijn-Plazzotta enumeration. In
particular, the study obtains an upper bound on the sequence providing
the smallest Colijn-Plazzotta rank assigned to some tree
with n leaves, and an asymptotic equivalence for the sequence
providing the largest Colijn-Plazzotta rank assigned to some tree
with n leaves.
12-2-2020 — Admixture inflates the genetic diversity of the
admixed population above that of the source populations — or does
it? Simina
Boca and Lucy
Huang explore the effect
of admixture on heterozygosity, examining when an admixed population
has heterozygosity greater than that of source populations. The study
also characterizes the level of admixture that gives rise to the
greatest heterozygosity for a given set of source population allele frequencies.
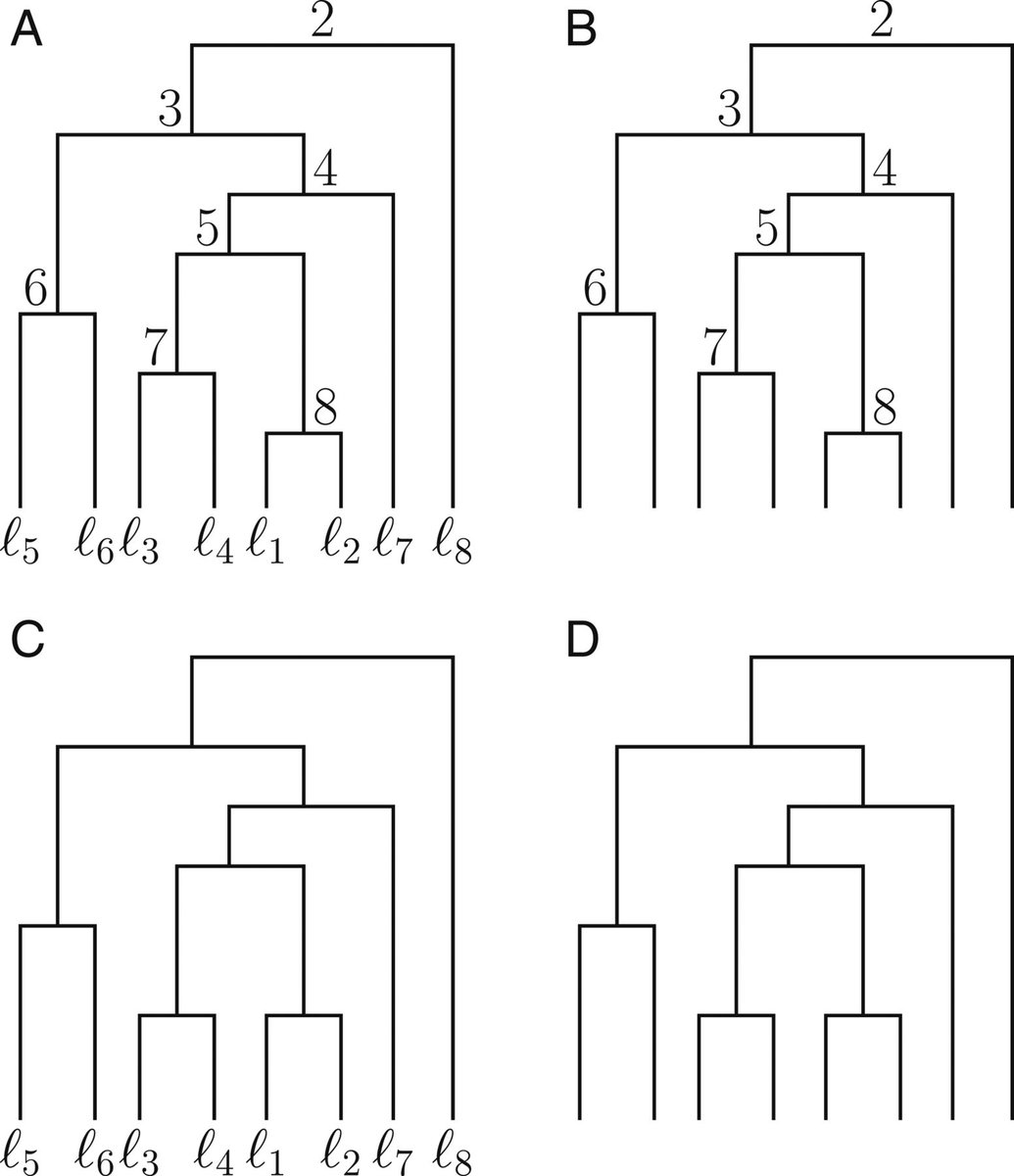
11-17-2020 — Studies of phylogenetic tree spaces have
often focused on unranked labeled trees (panel C below), unranked
unlabeled trees (panel D), or sometimes, ranked labeled trees (panel
A). In a
new study,
Jaehee Kim introduces metrics for calculating distances
between ranked unlabeled trees, an understudied type of
tree that is useful in tracking pathogen lineages (panel B). The
finds shows that the metrics can be used to cluster trees arising
from a shared generative model, and to distinguish between those
that have arisen by different models.
3-21-2022 — Alissa Severson and a collaborative
team report a
genetic study of ancient
burial sites and their continuity with modern members of the Muwekma
Ohlone Tribe. The project, a collaboration with the tribal leadership,
finds a component of genetic ancestry that connects two burial sites
separated by hundreds of years with each other and with the modern
tribal members.
[Illinois
News Bureau]
[Stanford
Report]
11-30-2021 — Under the coalescent model, a genealogical tree
possess a series of features: its height, length, sum of external
branches, sum of internal branches, and mean basal branch
length. Egor Alimpiev
has calculated the
covariance and correlation coefficients of all these pairs of random
variables, providing a compendium of existing and new fundamental results for the
coalescent model. The calculation builds on a previous calculation for one of
the pairs considered [154].
11-11-2021 — The Sackin index is one of the most
commonly used measures of tree balance. Undergraduate Matt King
reports a simple new proof
of a result that finds the mean value of the Sackin index across all
labeled topologies on n leaves. The proof makes use of an
identity that has been called by Graham, Knuth & Patashnik a
"remarkable property of the 'middle' elements of Pascal's triangle."
8-24-2021 — For a caterpillar species tree,
undergraduate Egor
Alimpiev studies
coalescent histories in a family of gene trees,
the p-pseudocaterpillar gene trees. For this family, his study
investigates a claim that the number of coalescent histories is affected
by a tradeoff between the number of possible sequences of coalescences
and the number of species tree branches on which those sequences can
take place. He finds a very nice symmetry. The work extends a study by a previous undergraduate in the
lab, Zoe Himwich
[176]
8-24-2021 — PhD student Danny
Cotter continues the
investigation of coalescence times in consanguineous populations,
considering the mean time to coalescence for a pair of lineages on the X
chromosome in each of four first-cousin mating models. He finds that
matrilateral first-cousin mating reduces X-chromosomal coalescence times
to a greater extent than patrilateral first-cousin mating. The work
builds on two studies led by co-author Alissa Severson
[166]
[194].
5-28-2021 —
In a new article led by PhD student
Alissa Severson, the distribution of coalescence times is computed
in a diploid model of a consanguineous population. Using a
separation-of-time-scales approach, the study shows that the time to the
most recent common ancestor for pairs of lineages in separate mating pairs
follows a coalescent model with a reduced effective popualtion size. The
study builds on a previous theoretical study that examined the mean
pairwise coalescence time
[166].
5-25-2021 — Congratulations! Alissa Severson has
successfully defended her PhD, "The effect of relatedness and population
structure on patterns of genomic sharing."
5-21-2021 — Jaehee
Kim, Doc Edge,
and Amy Goldberg report
a study of the decoupling of a
phenotype from admixture levels in an admixed population whose source
populations differed in phenotype. As time proceeds, the phenotype of
an individual comes to reveal less and less information about the individual's
admixture level, particularly if mating occurs randomly in the admixed population. [Stanford
Report]
3-11-2021
— Gili
Greenbaum and Jaehee Kim report a
population-genetic model
of gene drives and their potential to "spill over" from one population to
another. In the model, an engineered gene drive is introduced into a
target population with the goal of overtaking the extant population. Under
what circumstances can the introduced gene drive be prevented from
overtaking genotypes in non-target populations? The study finds a narrow
set of circumstances.
2-8-2021 — Last year
we celebrated
the 50th anniversary of the journal Theoretical Population
Biology. The anniversary came just as the role for mathematical
epidemiology models of COVID-19 began receiving intense attention. A
recent editorial discusses the
connections between decades of population biology modeling and the
COVID-19 pandemic.
2-2-2021 — In
a genome scan of rats in
New York City, former rotation student Arbel Harpak identifies
genes associated with metabolism, diet, the nervous system, and
locomotion as possible targets of natural selection. The results add
to a growing understanding of adaptation in human-commensal species.
12-18-2020 — Colijn & Plazzotta (2018) introduced a
clever new way to associate the unlabeled binary rooted trees with the
positive integers. A
new paper explores the
mathematical properties of the Colijn-Plazzotta enumeration. In
particular, the study obtains an upper bound on the sequence providing
the smallest Colijn-Plazzotta rank assigned to some tree
with n leaves, and an asymptotic equivalence for the sequence
providing the largest Colijn-Plazzotta rank assigned to some tree
with n leaves.
12-2-2020 — Admixture inflates the genetic diversity of the
admixed population above that of the source populations — or does
it? Simina
Boca and Lucy
Huang explore the effect
of admixture on heterozygosity, examining when an admixed population
has heterozygosity greater than that of source populations. The study
also characterizes the level of admixture that gives rise to the
greatest heterozygosity for a given set of source population allele frequencies.
11-17-2020 — Studies of phylogenetic tree spaces have
often focused on unranked labeled trees (panel C below), unranked
unlabeled trees (panel D), or sometimes, ranked labeled trees (panel
A). In a
new study,
Jaehee Kim introduces metrics for calculating distances
between ranked unlabeled trees, an understudied type of
tree that is useful in tracking pathogen lineages (panel B). The
finds shows that the metrics can be used to cluster trees arising
from a shared generative model, and to distinguish between those
that have arisen by different models.
 8-4-2020 — Alyssa Fortier and Jaehee Kim
examine the use of
ancestry inference as a step to improve relatedness profiling in
forensic genetics. By reducing the potential for misspecification of
allele frequencies in likelihood calculations, inference of the
genetic ancestry of the forensic sample can avoid a false positive
inference of relatedness.
7-29-2020 — Amy
Goldberg and Ananya Rastogi report
a study of "Assortative
mating by population of origin in a mechanistic model of admixture."
This work analyzes a model in which individuals mate assortatively
in a setting with two ancestral populations and an admixed
populaton. The study builds on several previous models from the lab.
[82]
[122]
[133]
6-11-2020 — Rohan Mehta reports an article entitled
"Modelling
anti-vaccine sentiment as a cultural pathogen." The paper
describes a coupled contagion: the spread of an anti-vaccine
sentiment, and the spread of the disease against which the
vaccine protects. The dynamics illustrate how spread of
sentiment against a vaccine generates and magnifies outbreaks of
the associated disease. [Stanford Report]
5-29-2020 — The long-awaited 50th anniversary
special issue of Theoretical Population Biology has been
published. The
special issue contains commentaries on major research areas developed
in TPB, commentaries on historic papers, biograpical
commentaries, and research articles — including
a study by Ilana
Arbisser on FST and the triangle inequality.
[Stanford Report]
4-24-2020 — Using a combination of coalescent
theory and simulation, Kim et
al. study the probability under a birth-death process that
species trees lie in the "anomaly zone," the region of the
parameter space in which species trees can disagree with the gene
tree they are most likely to produce. The work buils on earlier
studies of the anomaly zone
[30]
[47], ranked gene
trees [85]
[97], and joint
simulation of species trees and gene trees
[140].
3-20-2020 — A new
study examines the
mathematical connections between homozygosity and heterozygosity
statistics and measures of health care fragmentation in health
services research. The study relies on results from related studies in
the lab [87]
[158].
3-10-2020 — PhD graduate Jonathan Kang
reports a new study of
five measures of linkage disequilibrium. Jonathan computes
mathematical bounds on linkage disequilibrium measures in relation to
the allele frequencies at a pair of loci, analyzing the implications
of these bounds in human genetic data. The study builds on an earlier
analysis of the r2 measure
[51].
1-9-2020 —
A paper by Zoe
Himwich, recent Stanford graduate in mathematics, studies
coalescent histories for non-matching caterpillar gene trees and
species trees. This study in enumerative combinatorics identifies new
connections to the Catalan numbers, Dyck paths, and roadblocked
monotonic paths not crossing the diagonal of a square lattice. The
paper builds on two earlier studies of coalescent histories for
caterpillar-like tree families
[111]
[142].
12-9-2019 — Gili
Greenbaum introduces a new network-based approach
to inference of population structure. The method relies on
detection of "communities" in genetic distance matrices
and can be used to produce a new way of displaying
population structure — a "population structure tree."
12-8-2019 — The work of lab alumnus Brian Donovan
is featured on the front page of
the New
York Times.
8-4-2020 — Alyssa Fortier and Jaehee Kim
examine the use of
ancestry inference as a step to improve relatedness profiling in
forensic genetics. By reducing the potential for misspecification of
allele frequencies in likelihood calculations, inference of the
genetic ancestry of the forensic sample can avoid a false positive
inference of relatedness.
7-29-2020 — Amy
Goldberg and Ananya Rastogi report
a study of "Assortative
mating by population of origin in a mechanistic model of admixture."
This work analyzes a model in which individuals mate assortatively
in a setting with two ancestral populations and an admixed
populaton. The study builds on several previous models from the lab.
[82]
[122]
[133]
6-11-2020 — Rohan Mehta reports an article entitled
"Modelling
anti-vaccine sentiment as a cultural pathogen." The paper
describes a coupled contagion: the spread of an anti-vaccine
sentiment, and the spread of the disease against which the
vaccine protects. The dynamics illustrate how spread of
sentiment against a vaccine generates and magnifies outbreaks of
the associated disease. [Stanford Report]
5-29-2020 — The long-awaited 50th anniversary
special issue of Theoretical Population Biology has been
published. The
special issue contains commentaries on major research areas developed
in TPB, commentaries on historic papers, biograpical
commentaries, and research articles — including
a study by Ilana
Arbisser on FST and the triangle inequality.
[Stanford Report]
4-24-2020 — Using a combination of coalescent
theory and simulation, Kim et
al. study the probability under a birth-death process that
species trees lie in the "anomaly zone," the region of the
parameter space in which species trees can disagree with the gene
tree they are most likely to produce. The work buils on earlier
studies of the anomaly zone
[30]
[47], ranked gene
trees [85]
[97], and joint
simulation of species trees and gene trees
[140].
3-20-2020 — A new
study examines the
mathematical connections between homozygosity and heterozygosity
statistics and measures of health care fragmentation in health
services research. The study relies on results from related studies in
the lab [87]
[158].
3-10-2020 — PhD graduate Jonathan Kang
reports a new study of
five measures of linkage disequilibrium. Jonathan computes
mathematical bounds on linkage disequilibrium measures in relation to
the allele frequencies at a pair of loci, analyzing the implications
of these bounds in human genetic data. The study builds on an earlier
analysis of the r2 measure
[51].
1-9-2020 —
A paper by Zoe
Himwich, recent Stanford graduate in mathematics, studies
coalescent histories for non-matching caterpillar gene trees and
species trees. This study in enumerative combinatorics identifies new
connections to the Catalan numbers, Dyck paths, and roadblocked
monotonic paths not crossing the diagonal of a square lattice. The
paper builds on two earlier studies of coalescent histories for
caterpillar-like tree families
[111]
[142].
12-9-2019 — Gili
Greenbaum introduces a new network-based approach
to inference of population structure. The method relies on
detection of "communities" in genetic distance matrices
and can be used to produce a new way of displaying
population structure — a "population structure tree."
12-8-2019 — The work of lab alumnus Brian Donovan
is featured on the front page of
the New
York Times.
 11-1-2019
— Gili
Greenbaum reports a study of dynamics of the spatial boundary
between Neanderthals and Modern Humans before Modern Humans spread
rapidly out of Africa. The question is not "why did Modern Humans
replace Neanderthals so quickly?" Rather, Gili asks "why did Modern
Humans not replace Neanderthals for so long?" The proposed
answer lies in the
dynamics of infectious disease.
[Haaretz]
[Stanford Report]
10-1-2019 — A
new study by Rohan
Mehta computes probabilities under the coalescent model of
reciprocal monophyly for sets of gene lineages from three and four
species. The computation extends an earlier computation that permitted
only two sets of lineages
[141]. The study appears in a
special issue of Theoretical Population Biology celebrating
Marc Feldman's 75th birthday.
9-23-2019 — Nicolas Alcala studies the coalescent
theory of all possible symmetric migration models involving at most
four demes. His paper
examines coalescent quantities such as the time to the most recent
common ancestor under the models, determining how these quantities
relate to network properties such as the mean number of edges per
vertex and the density of edges. The study introduces a network
perspective for coalescent models — applying it to empirical
examples on tigers and birds of genus Sholicola in India. PhD
graduate Amy Goldberg also
contributed to the project.
9-9-2019 — A
new paper led by Rohan
Mehta examines the behavior of the FST measure of
genetic differentiation on haplotypic data. The study illustrates how
incrementing the length of the haplotype window tends to
decrease FST — but sometimes increases it. The
work is closely related to several of the lab's papers
on FST
[102]
[121]
[149]
[165]. Check out
the video
abstract drawn and narrated by co-author Alison Feder.
11-1-2019
— Gili
Greenbaum reports a study of dynamics of the spatial boundary
between Neanderthals and Modern Humans before Modern Humans spread
rapidly out of Africa. The question is not "why did Modern Humans
replace Neanderthals so quickly?" Rather, Gili asks "why did Modern
Humans not replace Neanderthals for so long?" The proposed
answer lies in the
dynamics of infectious disease.
[Haaretz]
[Stanford Report]
10-1-2019 — A
new study by Rohan
Mehta computes probabilities under the coalescent model of
reciprocal monophyly for sets of gene lineages from three and four
species. The computation extends an earlier computation that permitted
only two sets of lineages
[141]. The study appears in a
special issue of Theoretical Population Biology celebrating
Marc Feldman's 75th birthday.
9-23-2019 — Nicolas Alcala studies the coalescent
theory of all possible symmetric migration models involving at most
four demes. His paper
examines coalescent quantities such as the time to the most recent
common ancestor under the models, determining how these quantities
relate to network properties such as the mean number of edges per
vertex and the density of edges. The study introduces a network
perspective for coalescent models — applying it to empirical
examples on tigers and birds of genus Sholicola in India. PhD
graduate Amy Goldberg also
contributed to the project.
9-9-2019 — A
new paper led by Rohan
Mehta examines the behavior of the FST measure of
genetic differentiation on haplotypic data. The study illustrates how
incrementing the length of the haplotype window tends to
decrease FST — but sometimes increases it. The
work is closely related to several of the lab's papers
on FST
[102]
[121]
[149]
[165]. Check out
the video
abstract drawn and narrated by co-author Alison Feder.

 5-8-2019 — In a collaboration with
the Stanford Conservation
Program, we have developed a stochastic population occupancy model
to examine two decades of occupancy data from the campus populations
of the California red-legged frog (Rana draytonii). The model
seeks to explain population declines of R. draytonii in
campus creeks and suggests conservation management approaches for
reversing these
declines. The study was led
by Nicolas Alcala.
5-2-2019 — A
new study led by Alissa
Severson examines the relationship between runs of homozygosity
and identity-by-descent tracts. The paper determines for a diploid
coalescent model the time to the most recent common ancestor, both for
two haplotypes in the same individual and for two haplotypes in
different individuals. The work provides theory that builds on
empirical observations in an earlier study
[144].
4-29-2019 — Nicolas Alcala has a
new study of
mathematical bounds on three population-genetic
statistics: GST', Jost's D,
and FST. He shows that for biallelic markers whose
mean frequency across a set of populations is fixed, these three
statistics achieve their maximal values at the same configuration of
allele frequencies across populations. The results extend
Nicolas's earlier
work on FST bounds as well as that of two
other studies from the lab concerning bounds
on FST
[102]
[121].
3-26-2019 — Filippo Disanto reports
a study of the
enumeration of compact coalescent histories for matching gene
trees and species trees. Compact coalescent histories represent a
combinatorial structure that collapses standard coalescent histories
into a smaller number of equivalence classes. The study extends the
lab's work on enumeration of
coalescent histories to a new structure.
3-3-2019 — A
new paper discusses
challenges of interpreting differences in polygenic scores across
populations. The paper builds from the models developed by
Ph.D. graduate Doc Edge for
analyzing the relationship between the magnitude of genetic and
phenotypic differences among populations [129]
[132].
1-23-2019 — Two papers from the lab appear in a special
issue of Bulletin of Mathematical Biology on Algebraic
Methods in Phylogenetics.
5-8-2019 — In a collaboration with
the Stanford Conservation
Program, we have developed a stochastic population occupancy model
to examine two decades of occupancy data from the campus populations
of the California red-legged frog (Rana draytonii). The model
seeks to explain population declines of R. draytonii in
campus creeks and suggests conservation management approaches for
reversing these
declines. The study was led
by Nicolas Alcala.
5-2-2019 — A
new study led by Alissa
Severson examines the relationship between runs of homozygosity
and identity-by-descent tracts. The paper determines for a diploid
coalescent model the time to the most recent common ancestor, both for
two haplotypes in the same individual and for two haplotypes in
different individuals. The work provides theory that builds on
empirical observations in an earlier study
[144].
4-29-2019 — Nicolas Alcala has a
new study of
mathematical bounds on three population-genetic
statistics: GST', Jost's D,
and FST. He shows that for biallelic markers whose
mean frequency across a set of populations is fixed, these three
statistics achieve their maximal values at the same configuration of
allele frequencies across populations. The results extend
Nicolas's earlier
work on FST bounds as well as that of two
other studies from the lab concerning bounds
on FST
[102]
[121].
3-26-2019 — Filippo Disanto reports
a study of the
enumeration of compact coalescent histories for matching gene
trees and species trees. Compact coalescent histories represent a
combinatorial structure that collapses standard coalescent histories
into a smaller number of equivalence classes. The study extends the
lab's work on enumeration of
coalescent histories to a new structure.
3-3-2019 — A
new paper discusses
challenges of interpreting differences in polygenic scores across
populations. The paper builds from the models developed by
Ph.D. graduate Doc Edge for
analyzing the relationship between the magnitude of genetic and
phenotypic differences among populations [129]
[132].
1-23-2019 — Two papers from the lab appear in a special
issue of Bulletin of Mathematical Biology on Algebraic
Methods in Phylogenetics.
- Jaehee Kim, Filippo Disanto, and Naama Kopelman
report a study of the properties
of the neighbor-joining algorithm when applied to data from admixed
populations. The study shows that tree properties conjectured by
Kopelman et
al. [99] do
not necessarily hold for every distance matrix, but they do hold much more
frequently than in a null model without an admixed taxon.
- Filippo
Disanto examines the
number of nonequivalent ancestral configurations for matching gene trees
and species trees. Nonequivalent ancestral configurations at
first appear to be less numerous than ancestral configurations without
applying the equivalence relation — studied previously by Filippo
[152]. Here, Filippo
shows that asymptotic growth for nonequivalent configurations is also
exponential.
This pair of studies extends the lab's work
on theory of admixture and
combinatorics of evolutionary
trees.
Past news items
SELECTED RECENT PUBLICATIONS
X Liu, NM Kopelman, NA Rosenberg (2023) A
Dirichlet model of alignment cost in mixed-membership unsupervised
clustering. Journal of Computational and Graphical Statistics
32: 1145-1159. [Abstract]
[PDF]
[Supplement]
JA Mooney, L Agranat-Tamir, JK Pritchard, NA
Rosenberg (2023) On the number of genealogical ancestors tracing to
the source groups of an admixed population. Genetics 224:
iyad079. [Abstract]
[PDF]
[Supplement]
ML Morrison, N Alcala, NA Rosenberg (2022)
FSTruct: an FST-based tool for measuring ancestry
variation in inference of population structure. Molecular Ecology
Resources 22: 2614-2626.
[Abstract]
[PDF]
[Supplement]
E Alimpiev, NA Rosenberg (2022) A compendium of
covariances and correlation coefficients of coalescent tree
properties. Theoretical Population Biology 143: 1-13.
[Abstract]
[PDF]
J Kim, MD Edge, A Goldberg, NA Rosenberg
(2021) Skin deep: the decoupling of genetic admixture levels from
phenotypes that differed between source populations. American
Journal of Physical Anthropology 175: 406-421 (2021).
[Abstract]
NA Rosenberg (2021) On the Colijn-Plazzotta numbering scheme
for unlabeled binary rooted trees. Discrete Applied
Mathematics 291:
88-98. [Abstract]
[PDF]
RS Mehta, NA Rosenberg (2020) Modelling anti-vaccine
sentiment as a cultural pathogen. Evolutionary Human Sciences 2:
e21. [Abstract]
[PDF]
[Supplement]
IM Arbisser, NA Rosenberg (2020) FST
and the triangle inequality for biallelic markers. Theoretical
Population Biology 133: 117-129.
[Abstract]
NA Rosenberg (2020) Fifty years of Theoretical
Population Biology.
Theoretical Population Biology 133: 1-12.
[Abstract]
ZM Himwich, NA Rosenberg (2020) Roadblocked monotonic
paths and the enumeration of coalescent histories for non-matching
caterpillar gene trees and species trees. Advances in Applied
Mathematics 113: 101939.
[Abstract]
AL Severson, S Carmi, NA Rosenberg (2019) The effect of
consanguinity on between-individual identity-by-descent
sharing. Genetics 212: 305-316.
[Abstract]
[PDF]
NA Rosenberg, MD Edge, JK Pritchard, MW Feldman (2019)
Interpreting polygenic scores, polygenic adaptation, and human
phenotypic
differences. Evolution, Medicine, and Public Health 2019:
26-34.
[Abstract]
[PDF]
NA Rosenberg (2019) Enumeration of lonely pairs of gene
trees and species trees by means of antipodal
cherries. Advances in Applied Mathematics 102:
1-17. [Abstract]
[PDF]
J Kim, MD Edge, BFB Algee-Hewitt, JZ Li, NA
Rosenberg (2018) Statistical detection of relatives typed with
disjoint forensic and biomedical loci. Cell 175: 848-858.
[Abstract]
[PDF]
[Supplement]
|